ストレートフラッシュとは？出る確率や強さをわかりやすく解説

「ストレートフラッシュ」は、ポーカーで成立する役のうち、2番目のランクを誇るかなり強い役です。しかし最強役である「ロイヤルストレートフラッシュ」の影に隠れ、どれくらい強いのかピンと来ないという方も多いのではないでしょうか？

このページでは、ポーカーの役の一つであるストレートフラッシュについて解説します。ストレートフラッシュが成立する確率や、ロイヤルストレートフラッシュとの違いについても詳しく解説しているので、見分けが付かなくて困っている方も安心です！

Bell

(ウィナーズクラブ管理人)

ストレートフラッシュが引ければほぼ負けなし！というほどの強さがありますが、その分成立する条件も厳しいです。

最初にストレートフラッシュが配られる確率はなんと0.0014％！麻雀の地和よりも低い確率なので、なかなかお目にかかることがありません。

この記事はおよそ 7分 で読むことができます。時間がない方は目次を活用しましょう

ストレートフラッシュとは？

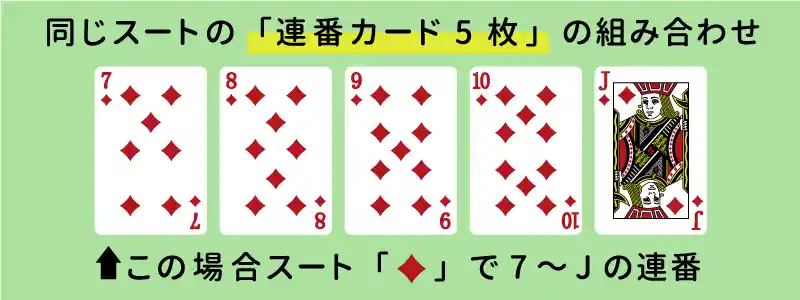
ポーカーの「ストレートフラッシュ（ストフラ）」とは、5枚のカードすべてが同じスート（絵柄）であることに加え、連番にもなっている役のことです。

• ストレート… 5枚のカードが全て連番になっている役（6・7・8・9・10など）
• フラッシュ… 5枚のカードが全て同じスート（スペードやハートなどの絵柄）になっている役

この両方の役を同時に満たす場合、ストレートフラッシュという役になります。

ストレートフラッシュの強さ

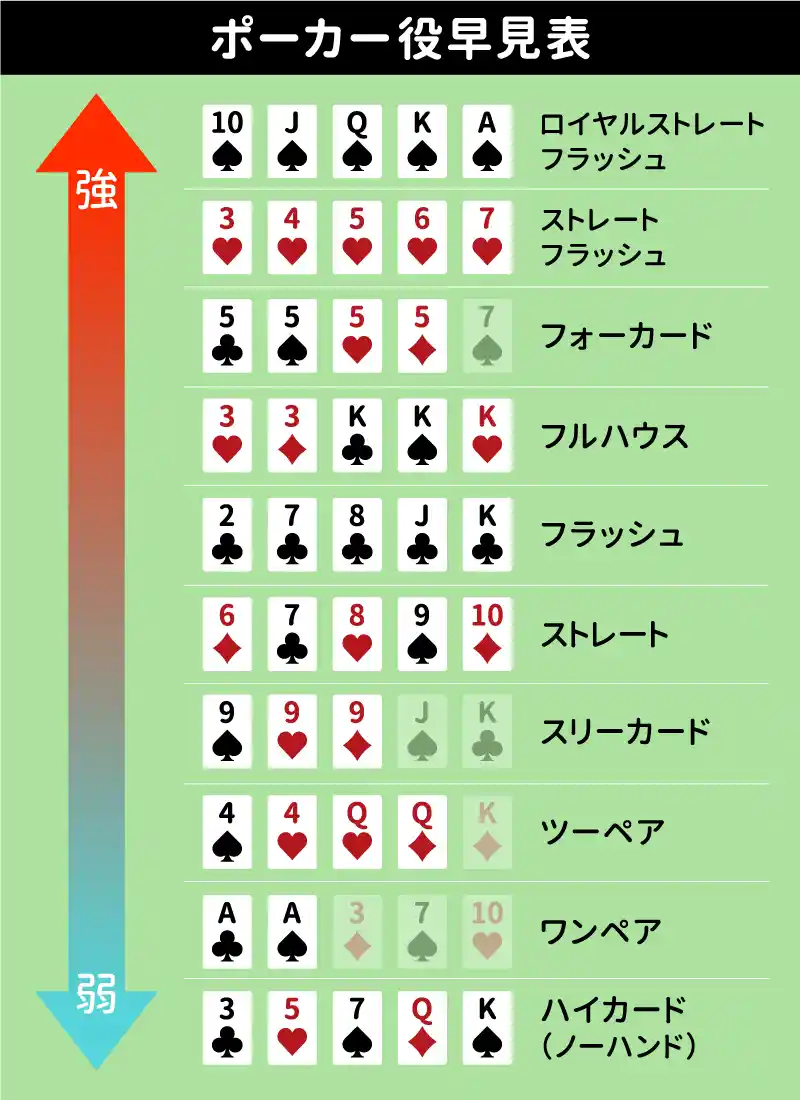
ストレートフラッシュの強さにあまりピンと来ない方も多いかもしれませんが、ポーカーの中で2番目に強い役です。最強役「ロイヤルストレートフラッシュ（ロイヤルフラッシュ）」以外の全ての役に勝つことができます。

例えば強役として知られるフォーカードやフルハウスよりもストレートフラッシュのほうが強い役となっており、出現確率についても桁が違います。かなり希少な役と考えておくと良いでしょう。

ストレートフラッシュが出現する確率

ここでは、「最初にストレートフラッシュが配られる確率」について解説します。

ストレートフラッシュが成立するパターンを♠︎だけで考えてみると

• A♠︎・2♠︎・3♠︎・4♠︎・5♠︎
• 2♠︎・3♠︎・4♠︎・5♠︎・6♠︎
• …
• 9♠︎・10♠︎・J♠︎・Q♠︎・K♠︎

の9通りです。

これがスペード、ハート、ダイヤ、クラブの4スートあるので、パターンの総数は 9 × 4 = 36 通りとなります。

トランプ52枚から5枚のカードを順番を問わず選ぶ場合の数は
52C5 =（52×51×50×49×48）÷（5×4×3×2×1）＝ 2,598,960 通りとなります。

正確な確率を求めるのは難しい

ちなみに、ストレートフラッシュが完成する確率を正確に計算するのはかなり難しいと言えます。

例えば「9♣・10♣・J♣・Q♣・K♣」という組み合わせが最初に配られた時、ストレートフラッシュで確定させますか？それとも、ロイヤルを狙って9♣を交換しますか？

このように、ストレートフラッシュが最終的に成立する確率というのは人によって異なります。

カードの組み合わせ例

ストレートフラッシュは文字通りストレートとフラッシュを合わせた役なのですが、それだけ言われてもピンと来ないかもしれません。

そこで、次の項目では「この組み合わせがストレートフラッシュ」という例を説明します。

手札の5枚とも同じスートで数字が連番になっている

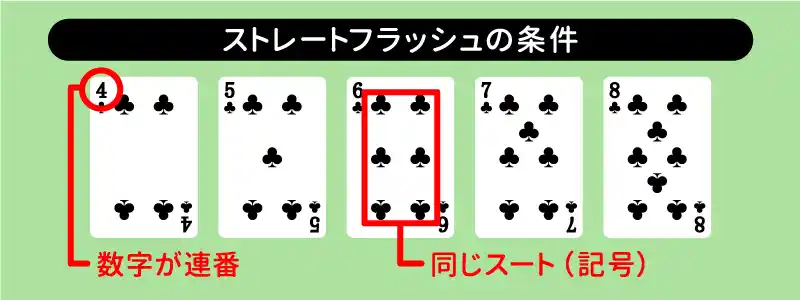
ストレートフラッシュを一言で説明すると「5枚とも同じスートで数字が連番になっている」組み合わせのことを指します。

例えば【4♠︎・5♠︎・6♠︎・7♠︎・8♠】️や、【8♦・9♦・10♦・J♦・Q♦】️などの組み合わせはストフラです。

ただし、【6♠︎・7♠︎・8♣・9♠︎・10♠】️などのように、1枚でも同じスートでなかったり数字が連番で無かった場合はストレートフラッシュにはなりません。この例では単にストレートとなります。

最強役のロイヤルフラッシュ

なお、こちらもストレートフラッシュではあるのですが、「10♠︎・J♠︎・Q♠︎・K♠︎・A♠︎」といった「10・J・Q・K・A」の組み合わせだけは例外です。

10〜Aの連番、なおかつ同じスートの場合は「ロイヤルストレートフラッシュ」と呼ばれます。ロイヤルストレートフラッシュはポーカーにおける最強役であり、ストレートフラッシュであっても勝つことはできません。

ストフラもロイヤルも狙える状況なら、積極的にロイヤルを狙う方が期待値が高くなる場合もあります。

ストレートフラッシュにならない例

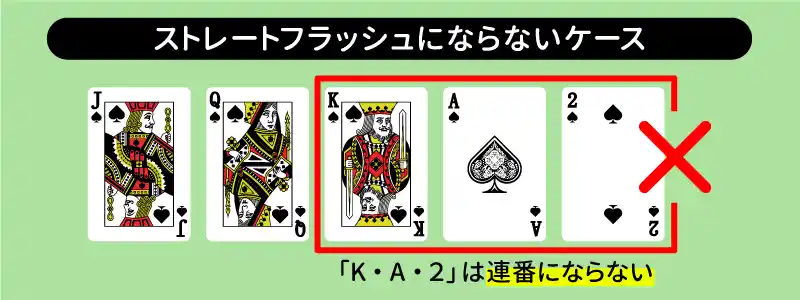
ストレートフラッシュでは連番が条件の一つとなっています。このうち、「A（エース）」という数字は特殊で、Kの1個後としても2の1個前としても使うことができるのですが、「K-A-2」と跨いで使うことはできません。

そのため、
【J♠︎・Q♠︎・K♠︎・A♠︎・2♠︎】
【Q♦・K♦・A♦・2♦・3♦】
などの組み合わせについてはストレートフラッシュと考えることはできません。

ただし、
【A♠︎・2♠︎・3♠︎・4♠︎・5♠︎】
などA〜5の組み合わせについては、K-A-2の組み合わせが入っていないためストレートフラッシュとして認められます。

ストレートフラッシュ同士の勝敗

対プレイヤーのポーカーの場合、成立役のランクが高い方が勝者となります。しかし、もしプレイヤーが両方ともストレートフラッシュだった場合、どのように勝敗が決まるのでしょうか？

二人ともストフラだった場合、勝敗は「5枚の中でもっとも大きい数字」によって決まります。

例えばプレイヤーが「4♠︎・5♠︎・6♠︎・7♠︎・8♠︎」と「5♠︎・6♠︎・7♠︎・8♠︎・9♠︎」で争っている場合、9♠︎を持っている方が勝者となります。

そんな状況あるのか？ と思われるかもしれませんので、このようなテキサス・ホールデムのシチュエーションを考えました。

ストレートフラッシュ同士の勝負になる具体的な例

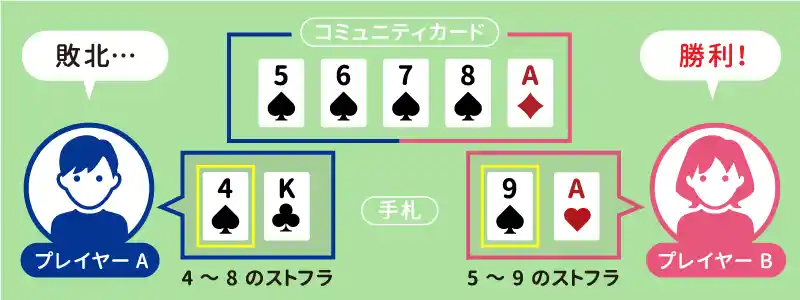
• コミュニティカード「5♠︎・6♠︎・7♠︎・8♠︎・A♦」
• プレイヤーAの手札「4♠︎・K♣」
• プレイヤーBの手札「9♠・8♥︎」

この場合、プレイヤーAとしては4♠︎・5♠︎・6♠︎・7♠︎・8♠︎のストレートフラッシュが成立しているので、負けることは無いように思えるかもしれません。

しかし、実はプレイヤーBが「9♠︎」を持っており、5♠︎・6♠︎・7♠︎・8♠︎・9♠︎のストレートフラッシュが成立するため、4♠︎を持っているプレイヤーAは負けてしまいます。

このように、ストレートフラッシュが成立していても、負けるケースは少なくないためご注意ください。

まとめ

ストレートフラッシュは、「ロイヤルフラッシュ」に次ぐポーカーで2番目がランクが高い役です。

実はロイヤルフラッシュの出現確率はかなり低く、配られた段階では7万分の1しかありません。そのためフォーカードやフルハウスなどの上位役よりも格が高い成立役となっています。

ほとんどの場合対人ポーカーでは勝つことができますし、ビデオポーカーでもかなりの配当を獲得できるので、積極的に狙う方が良いでしょう。

ただし、同じくらいの確率でロイヤルもストフラも狙えるようであれば、ロイヤルフラッシュを狙った方が最終的な収支が安定するためおすすめです。